Numerika preprostega primera

Primerjava numeričnega in analitičnega preračuna obremenjene palice okroglega prereza

V inženirski praksi se pri numeričnih trdnostnih preračunih pogosto želimo z rezultati čim bolj približati vrednostim analitičnega preračuna. Da bi se rezultati popolnoma ujemali, je seveda praktično nemogoče, saj že s samo uporabo metode končnih elementov (v nadaljevanju MKE) vnesemo določen delež napake, ki pa je ob ustrezni kvaliteti mreže zanemarljiv. Tako se izkaže, da se lahko pri zelo enostavnih primerih z rezultati približamo analitičnim vrednostim pod 1%, seveda ob ustreznih prilagoditvah. Kot preprost primer lahko predstavimo palico, ki je torzijsko obremenjena, glede na prijemališče sile pa se v njej pojavi tudi upogibni moment, kot prikazani na sliki 1.1.

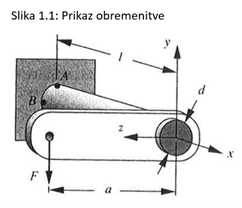
Napetostni stanji, nas zanimata v tem primeru se nahajata v točkah A in B. Tako se v točki A pojavi napetostni stanje maksimalnih normalnih napetosti, medtem, ko se v točki B pojavi stanje največjih strižnih napetosti. V točki A se torej material najbolj upira proti upogibni obremenitvi – ker je točka A najbolj oddaljena od prijemališča sile, tam nastanejo največje normalne napetosti. V točki A se prav tako pojavijo tudi strižne napetosti, ki pa so v veliki meri posledica torzijske obremenitve. Prispevek napetosti zaradi strižnih notranjih sil, ki delujejo v navpični smeri je manjši, saj se točka A nahaja na vrhu krožnega profila. V točki B je prispevek napetosti zaradi upogibne obremenitve praktično zanemarljiv, saj omenjena točka leži praktično na nevtralni osi. Tukaj se tako pojavijo največje strižne napetosti v vertikalni smeri, ki se na eni strani profila seštejejo z torzijskimi napetostmi, na drugi strani pa odštejejo. Tako lahko za obe točki zapišemo komponente napetostnih tenzorjev, kot prikazuje slika 1.2.

Če se analitičnim rezultatom želimo približati z numerično analizo, je potrebno izločiti nekatere dejavnike, ki niso zajeti pri analitičnih postopkih. Tako za namene boljšega ujemanja rezultatov zapišemo kot materialni parameter z vrednostjo Poissonovega števila nič, saj bo tako potek napetosti bolj skladen z analitičnimi vrednostmi, ki so zgolj povprečne. Ob modeliranju geometrije, kot je prikazana na sliki 1.1, bi ob pregledu rezultatov naleteli na problematiko singularnega področja, za katerega je znano, da bi napetosti limitirale proti neskončnosti z zmanjševanjem velikosti končnih elementov. Omenjeno dejstvo je posledica tega, da MKE programi na mestu fiksnega vpetja predpišejo neskončno togost v vsa vozlišča. V izogib temi je potrebno geometrijo modelirati na način členkastih podpor. Na ta način modeliramo dvojno geometrijo palice, kar prikazuje slika 1.3, zato moramo posledično prilagoditi tudi obremenitve.

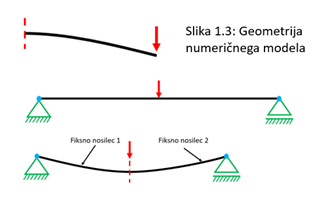
Pri gradnji numeričnega modela upoštevamo ustrezne toge povezave, prav tako z deljenjem geometrije predpišemo silo točno v vozlišče na težiščni osi palice. Na mestu, kjer želimo bolj natančno izračunati vrednosti, zgostimo mrežo končnih elementov, pri tem pa za globalni model upoštevamo velikost, ki je bila izbrana iz predhodno opravljene konvergenčne analize. Po ustrezni pripravi numeričnega modela lahko simulacijo zaženemo, nato pa sledi validacija dobljenih rezultatov. Primer numeričnega rezultata z napetostnimi tenzorji vidimo na sliki 1.4.

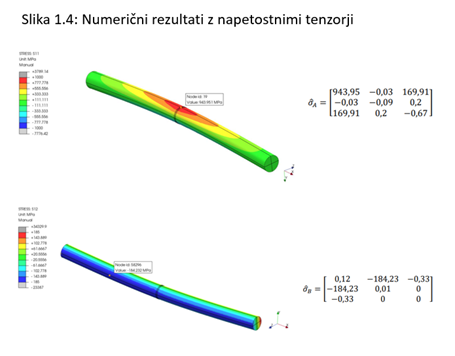
Tenzor napetosti je v obeh primerih približno enak analitičnemu. Minimalne vrednosti se kot posledica mreže pojavijo tudi v analitično ničelnih komponentah. Pri tem je upoštevano, da je napetostni tenzor simetričen čez diagonalo. Meritev za točko A tako izvedemo na predvidenem mestu, kar pa ne moramo izvesti za točko B. Razlog je ta, da v primeru numerične analize strižna sila v sredini ne zamenja predznaka v enem prerezu, ampak se to zgodi na določenem območju. Skladno s tem je potrebno meritev izvesti nekoliko iz sredine, kjer pa bo rezultat zaradi konstantne strižne napetosti v eni vzdolžni ravnini približno enak analitičnemu. Na ta način lahko v praksi uporabimo primerjavo rezultatov z analitičnim preračunom zgolj za validacijo numeričnega modela. Simulacijo je nato potrebno izvesti še z točnimi materialnimi parametri.